Introduction
Nixie tubes have been out of production for several decades, causing their trade prices to skyrocket. More recently, the revival of this technology has put tube lifetime under the spotlight once again; a topic of great and continuing interest to the hobbyist and commercial product designer alike.
At SALTechips, many of our customers ask us how long we expect these tubes to last. To provide them with an authoritative answer, as well as advance the knowledge amongst the nixie community, we designed the SALTechips IN-13 Endurance experiment (SHINE).
Our aim with the experiment was to measure the dimming of a standard IN-13 neon indicator tube over time. The loss of brightness is measured and used as an objective measure of the lifetime of the tube. Instead of overdriving the tube to accelerate darkening, we used normal operating conditions over a (very) long period of time. This allowed us to measure the rate at which the tube is becoming darker during normal operation and so have an objective measure of its lifetime.
Results
The experiment ran for approximately 2.7 years, at which point we stopped as we had adequate data to calculate the expected lifetime. In this section we present and discuss our results.
First off, let’s look at what happened to the tube itself and compare it to an unused tube. We will be referring to the tube used in the experiment as the SHINE tube. In figure 1, the fronts of the SHINE and new tubes can be seen. Although there is no immediate difference, one can see that the glass envelope has indeed become darker, for example near the yellow band. Also noteworthy is that the tube has become darker beyond where the glow ended (approx. three quarters from the right) although less so.

In figure 2 when looking at the back there is hardly any difference noticeable, at least with the tubes switched off.

Now let’s see the tubes switched on. In figure 3 we see that the glow of the new tube is more saturated whereas that of the SHINE tube is more subdued and darker. Beautiful nevertheless!

The most striking difference can be seen at the back of the tubes in figure 4. Unlike looking at the cathode glow through the front anode mesh electrode (figure 3), there is an aperture at the back of the tube and along its length allowing us to view the cathode glow directly through the darkened envelope. The much lower darkening of the front compared to the back is not by accident, but by design. As explained in (Stocker 1961), (Weston 1968) and other glow-discharge literature of the era, the mesh-style of the anode electrode reduces the darkening to an area less than the openings in the mesh. The overall effect is that the tube remains brighter when viewed from the side of the mesh i.e. the front. Finally, we note that the auxiliary electrode at the base of the tubes (far right) is no longer visible from the back of the SHINE tube but it is from the front (figure 4).

Moving onto the numerical results and beginning with figure 5, we plotted the raw measurement data for the entire duration of the experiment, 142 weeks. These are the measurements from step #11 in the experimental methodology. Here, the measured voltage is proportional to the brightness of the tube. The maximum voltage is 9.8253 Volts and the minimum 8.1390 Volts. This reduction represents a 17% loss of brightness during 2.7 years of continuous operation.
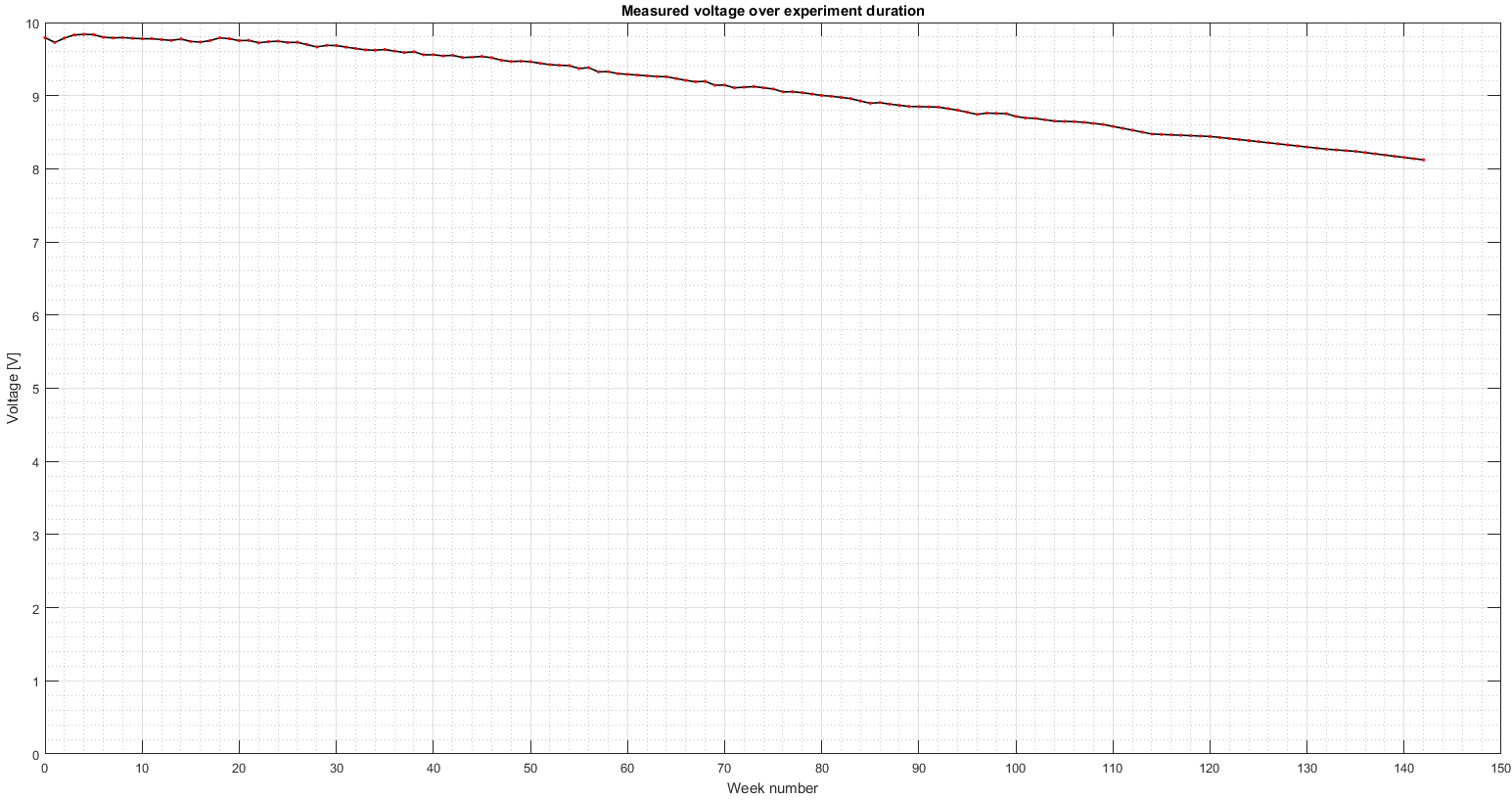
Continuing with figure 6, we felt it was beneficial for the subsequent optical density calculation (logarithm) to ‘smooth’ the raw measurement data a bit. So we applied a moving average filter with a window size of 4, corresponding to 1 month of collected data. The resulting data is shown in figure 6.
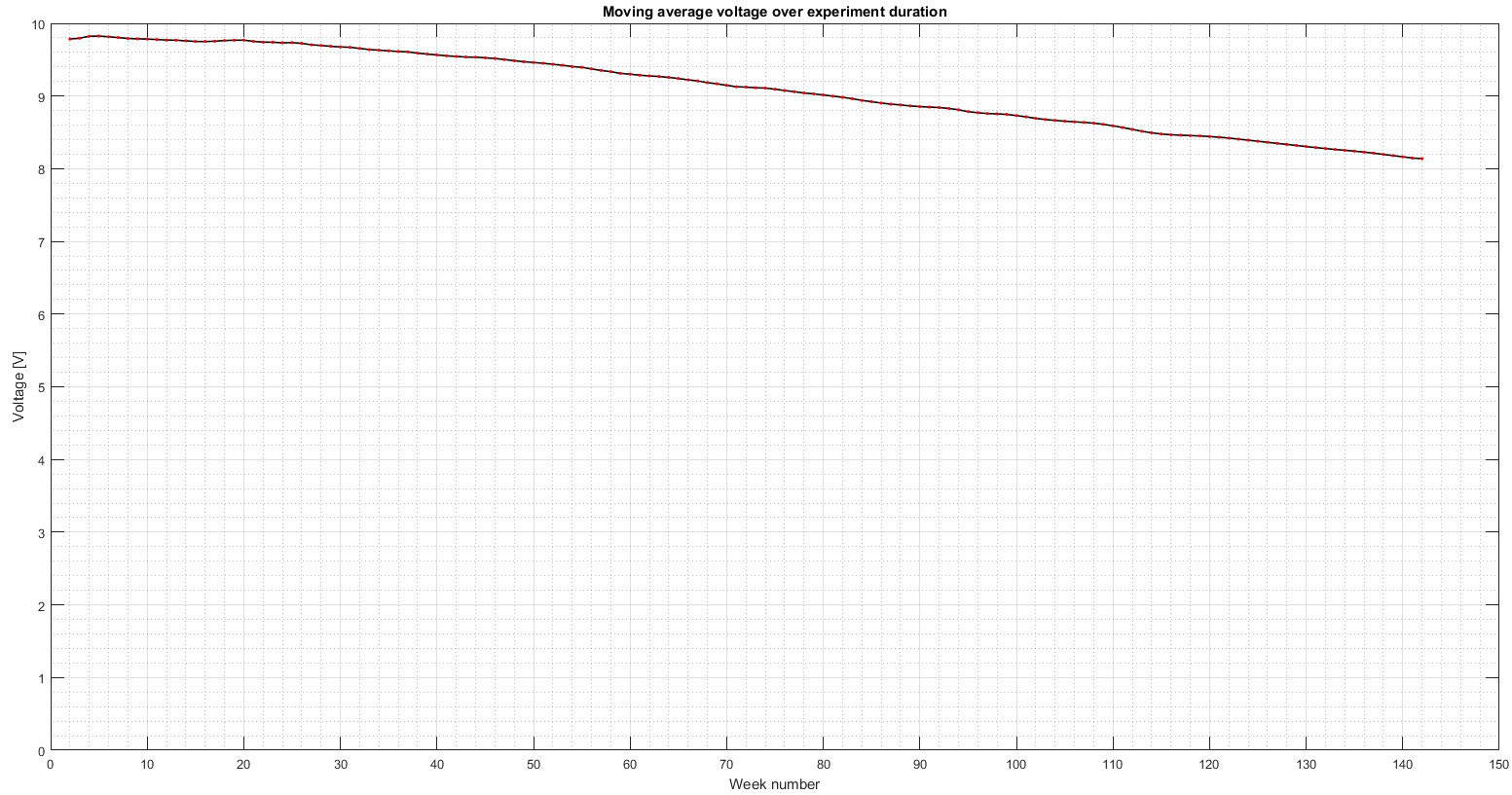
Using the filtered measurements we were able to compute the optical density of the glass wall over the experimental period. To do this we used equation [2] in §Theory and set Ir(t=0) equal to the maximum voltage in the dataset, 9.8253 Volts. The results are shown in figure 7. Examining figure 7, a quasi-linear part can be seen on the right and a quasi-quadratic part on the left. The transition occurs at approximately 40 weeks into the experiment. According to to our §Theory, our logarithmic model predicted a linearly increasing optical density over time, consistent with the right half of the plot. The discrepancy was also observed by Stocker back in 1961 (Stocker, 1961) who attributed it to “probably due to irregularities in the thin films”. Although this statement is plausible, we suspect that an additional factor is measurement error amplified by the logarithmic operation. Nevertheless, the fact that we also see the same discrepancy is confirmation that our experiment and analysis are valid. In any case, it is the linear part that we are interested in in order to calculate the tube’s lifetime.
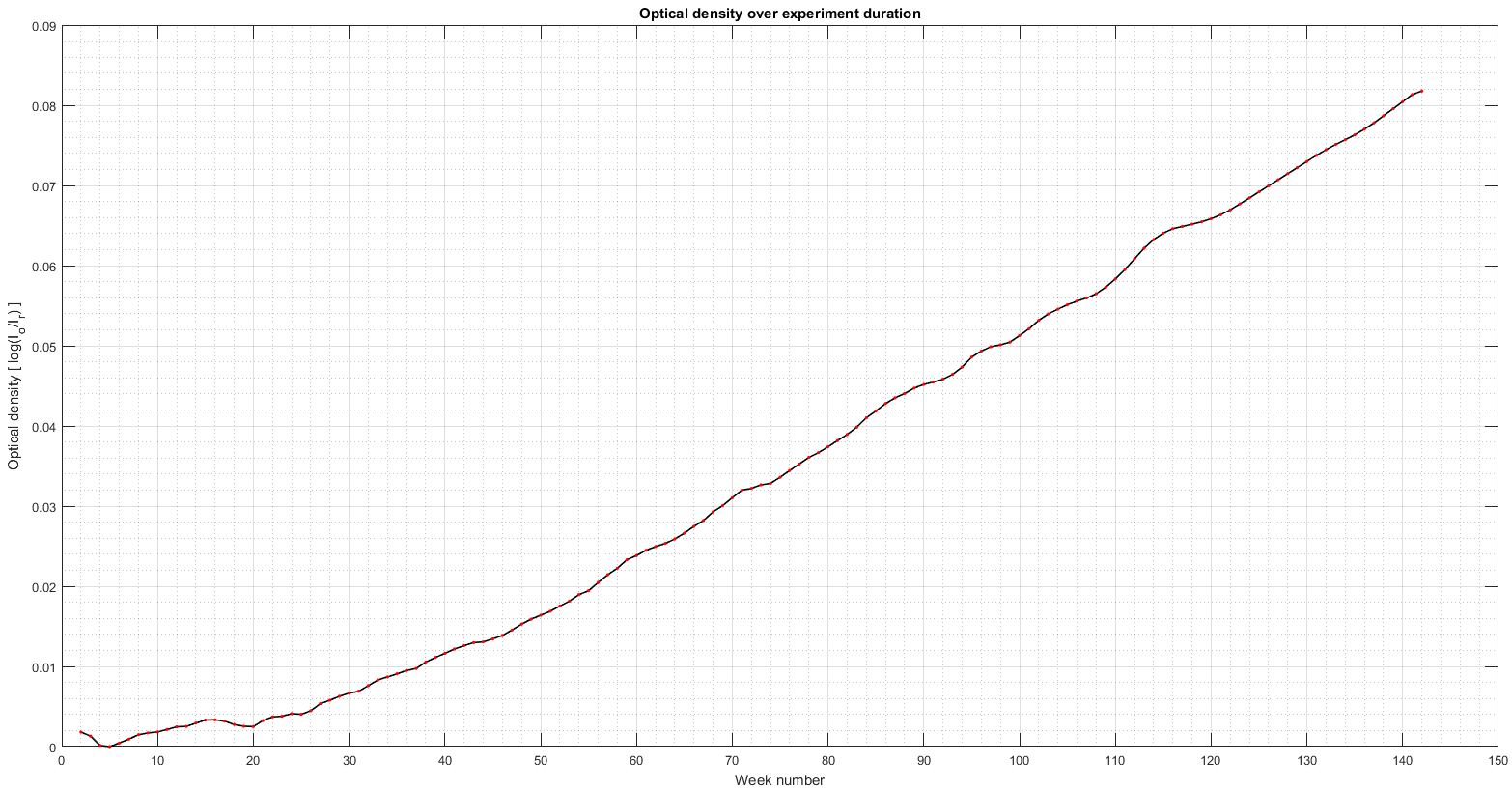
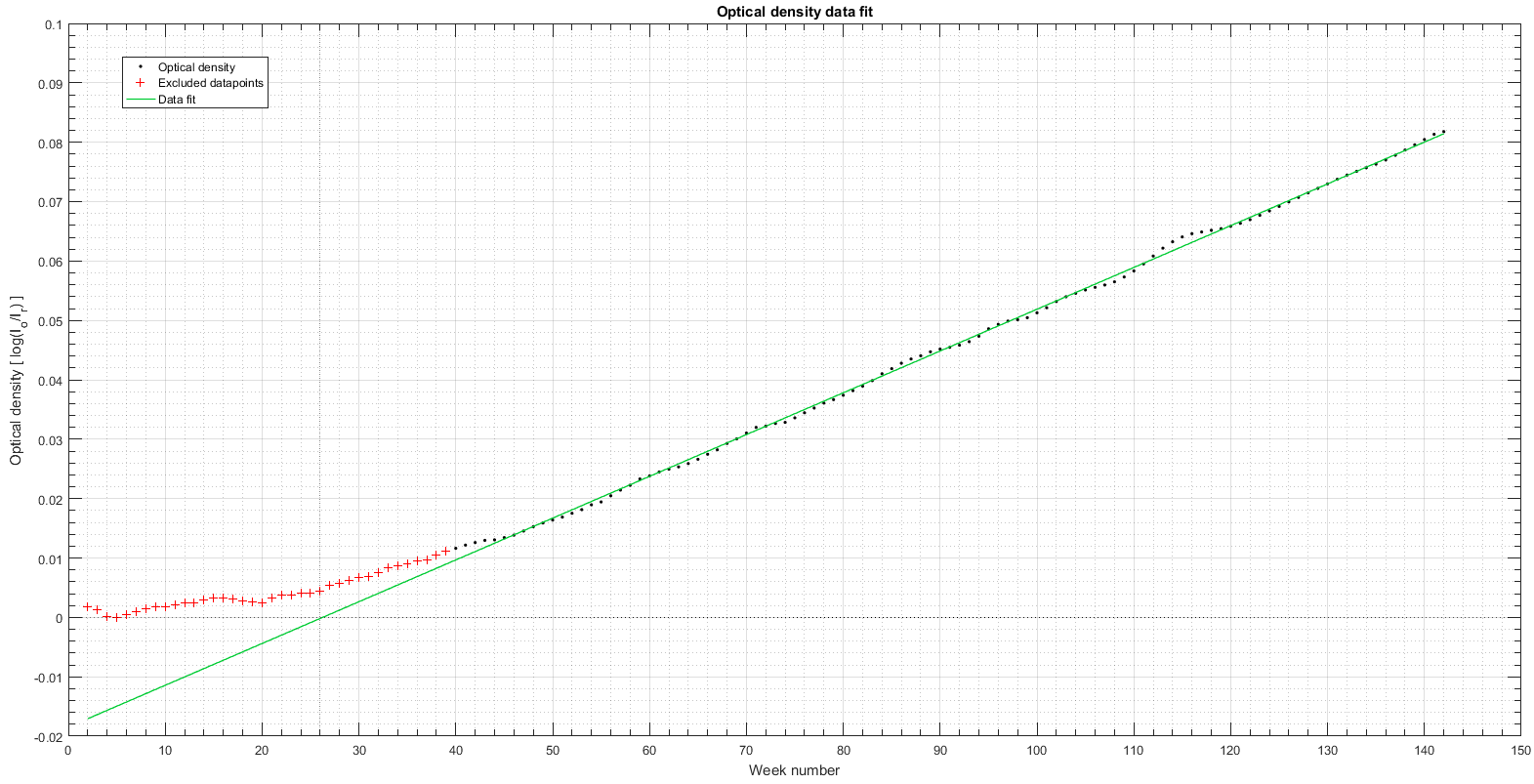
The equation of the linear line fit is:
D(t) = 0.0007035 * t – 0.01847 [5]
Where D(t) is the optical density at time t given in weeks. Equation 5 is a powerful tool that we can use to predict the brightness of the tube into the future, well past the 2.7 years we run the experiment for.
Lifetime Estimation
As described in the Theory section, we set a 30% brightness cutoff threshold to mark the end of life of the tube. Substituting equation 3 in equation 2, we can determine the optical density at the tube’s end of life:
D(t=end of life) = -log(0.3) = 0.5229 [6]
Substituting equation 6 in equation 5 and rearranging, we computed the time to reach that optical density:
(t=end of life) = (0.5229 + 0.01847) / 0.0007035 = 769 weeks = 14.7 years
That’s the magic number! We have estimated that it will take a whooping 14.7 years for the tube’s brightness to drop to 30%! That is a very long time indeed…
As far as the thermNeon is concerned, the temperature display algorithm will double the tube’s lifetime, increasing it all the way to 29 years! Mind-boggling.
Factory Sputtering
To determine how much sputtering was done at the factory, we once again used equation 5, setting D(t) = 0 and solving for time t.
0.0007035 * t – 0.01847 = 0, therefore t = 0.01847 / 0.0007035 = 26 weeks
We have estimated that the initial sputtering is equivalent to 26 weeks of normal operation. Needless to say, it did not take 26 weeks to make an IN-13 tube back in the day; the factory simply accelerated the sputtering process down to seconds by greatly overdriving the tube.
Theory
Failure mechanisms for cold-cathode discharge tubes
Mechanical damage
Cold cathode tubes are fragile structures of metal and ceramic components in a glass envelope.
Mechanical damage can occur due to impact or vibration. High levels of vibration can disjoint or bend internal structures. However, as such high vibration levels are in practice created by an impact, the glass envelope is likely to break first. The gas evacuation nipple is particularly susceptible to damage.
The glass-metal seals formed at the electrical connection pins can crack under excessive stress due to small-radius bending or local heating (e.g. when soldering).
Mechanical damage can also occur if excessive current is allowed to flow through the glow discharge, melting the electrodes or causing the envelope to explode from excessive internal pressure.
The effects of mechanical damage are usually catastrophic, irreversible and abrupt.
Contamination of gas mixture or electrodes
Contamination of the gas mixture or electrode surface alters the electrical characteristics of the tube. Standard tube driving circuits are unable to detect such deviations, therefore if the contamination is severe it can lead to unacceptable display inaccuracy and the tube being discarded.
Outgassing of the glass envelope is a source of contaminants. At temperatures developed in a cold cathode tube, the outgassed mixture of common soda-lime glass is 98% pure water vapour (Todd, 1955).
Outgassing also occurs at the electrodes by absorption (Malev, 1972) and adsorption of gas atoms (Moraw, 1986).
The effects of contamination are gradual and reversible in most cases. For this purpose cathodic sputtering is broadly used at the time of manufacture but also periodically during operation.
Cathode material deposition
During operation of the tube, cathode material is deposited on the glass envelope and internal surfaces. The process, known as sputtering, is due to the ejection of cathode material in the form of uncharged atoms as a result of bombardment by gas ions from the glow discharge. It is detrimental to the light output of the tube and for indicator tubes it can signal the end of their usable life.
A side-effect of sputtering is the formation of conductive films on insulating surfaces, leading to parasitic current paths that can interfere with normal operation. This was the subject of a different study.
The amount of sputtered material depends on ion density, ion energy, gas pressure, angle of impingement on the cathode and time. In a standard cold cathode tube the ion energy can vary between zero and that of the cathode fall, the ion density is linked to the gas pressure and ions can impinge on the cathode at random angles. What is more, the gas pressure is sufficiently high for most of the ejected material to be back-diffused to the cathode. As a result, rigorous modelling of sputtering in a glow discharge is challenging and experimental results are sparse.
Traditionally, theories on sputtering were developed using purpose-built tubes at low gas pressures. The sputtering yield i.e. the mean number of sputtered atoms per incident ion was measured by weighting the cathode electrode, measuring its resistance, or measuring the change in light transmittance of a transparent target. The results were then extrapolated for higher pressures present in glow discharges. Nevertheless, cathodic sputtering remained a popular research topic when glow discharge tubes were mainstream and entire chapters were devoted to the subject in literature of the time.
Of most relevance to this experiment is the work by Stocker, measuring the rate of deposition of molybdenum films in inert gases over the pressure range of 3-21 torr. The gases used included a Penning mixture of 99% neon and 1% argon (Stocker, 1961).
The sputtering rate was inferred by measuring the change of optical density of the tube’s glass wall as cathode material was deposited over time. Optical density D is a measure of how transparent a material is. It is defined as the logarithm of the ratio of the light intensity Io falling upon the material and the intensity Ir that is transmitted through the material. At time t, the optical density is given by:
D(t) = -log(\frac{Ir(t)}{Io}) [1]
Note that by definition Io is a constant equal to Ir(t) when t = 0 i.e. at the beginning of the experiment. Therefore equation [1] can be rewritten as:
D(t) = -log(\frac{Ir(t)}{Ir(t=0)}) [2]
Stocker observed that the optical density increases linearly with time as material is deposited, meaning that transmitted light intensity falls exponentially as it asymptotically approaches zero. In other words, the tube will become dimmer with time, doing so increasingly slower. In the SHINE experiment we adopted a slightly modified version of this model, described further below.
In order to determine the end of usable life of the tube, a stopping intensity threshold must be set. Below the threshold the tube will not be bright enough for its intended application. In the SHINE experiment we quasi-arbitarily selected an intensity cutoff threshold of 30%, considering that glow discharge tubes are nowadays primarily used indoors and the sensitivity of the human eye is quasi-logarithmic, meaning that lower light levels can easily be seen.
Therefore, at some time t the intensity cutoff threshold will be reached. At that time:
Ir(t) = 0.3 Ir(t=0) [3]
Another factor to take into consideration is that a sputtering cycle takes place during manufacturing of the tube, hence some material is already deposited on the walls. Therefore, the neon glow inside the tube is less than maximum even when the tube is new. This initial darkening is significant and must be accounted for in our model. We do this by modelling the initial optical density as a constant C. The new model then becomes:
D(t) = -log(\frac{Ir(t)}{Ir(t=0)}) + C [4]
Since we expect the optical density to increase linearly as a function of time (constant deposition rate), equation [4] is of the form y = mx + c, where
- y = D(t),
- m = -log(\frac{Ir(t)}{Ir(t=0)}),
- x = t and
- c=C.
The numerical objective of the experiment then was to determine parameters m and c. Doing so enabled us to ‘see into the future’ (extrapolate) to find after how much time the received intensity will reach the stopping threshold of 30%. Moreover, parameter c indicated how much sputtering was done at the factory at the time of manufacturing!
The theoretical model described is general and independent of effects such as gas composition, pressure, current, electrode material etc. Therefore the same model can be used with other glow discharge tubes such as IN-9, IN-18, B7971, IN-8…
Equipment
A diagram of the experimental setup we used is shown in figure 9. The HV power supply was a standard regulated 140 Volt output switch-mode power converter. It provided power to the neon tube via a constant current sink of similar design to the subcircuit used in the thermNeon.
Current through the tube is set so that approximately 50% of the tube’s length is illuminated. That way a sufficient illumination length is available for measurement, yet small drift of the driving current will not cause the tube to enter the abnormal glow operating region where sputtering is increased.
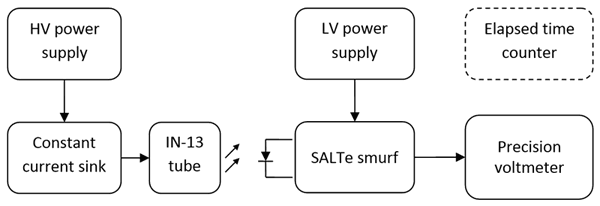
The intensity of the light emitted by the tube was measured by a custom transducer which we named SALTe smurf – because we made it, it is cute and blue! The SALTe smurf is a precision, ultralinear, low noise photometer designed specifically for this application by SALTechips. The current design has a dynamic range of 112 dB and a total output noise of 24 μV RMS. The output of the SALTe smurf is a voltage signal directly proportional to the light intensity of the tube. The photo sensor and tube were optically coupled by mounting of the tube immediately on the sensor as it can be seen in figure 10. The front of the tube was oriented towards the sensor and locked in place using foam.

The output of the SALTe smurf was measured with an HP-34401A multimeter connected via a short length of coaxial cable (RG-58U). The multimeter is configured as follows:
- DC Volts, autoranging
- 6.5 digit resolution, ‘slow’ integration time (2s @50Hz)
- Input impedance 10 MOhm
- Calibrated by the manufacturer before the experiment started and when it finished.
As the output signal from the SALTe smurf is linearly proportional to the light intensity of the tube, a 70% light intensity drop is marked by a 70% decrease in output voltage.
Methodology
| Step | Action | Status |
| 1 | Power up all equipment except the tube | done |
| 2 | Allow warm up time (~6h) | done |
| 3 | Record ambient temperature | done |
| 4 | Record output voltage offset (tube OFF) | done |
| 5 | Power up tube and adjust illumination length to 50% | done |
| 6 | Allow settling time (~30mins) | done |
| 7 | Record ambient temperature | done |
| 8 | Record maximum output voltage (tube ON) | done |
| 9 | Reset elapsed time counter | done |
| 10 | Enable live feed | done |
| 11 | Record output voltage every week | done |
| 12 | Repeat step 11 until end condition is reached (brightness down to 30%) | done |
| 13 | Calculate lifetime | done |
| 14 | Calculate sputtering from factory | done |
| 15 | Publish results | done |
Table 1: List of experimental steps of the SHINE experiment
Conclusions
The SHINE experiment has been a practical measurement of the lifetime of a typical neon indicator tube. In the past, predicting this behaviour has been speculative or inaccurate. We developed a theoretical basis, precision measurement instrumentation and a realistic experiment for this purpose. The experiment, which run for 2.7 years, focused on the IN-13 bargraph tube. However, the tools and techniques can readily be used on other glow discharge tubes.
We calculated that, unless there is some other extraordinary failure, the usable life of a typical IN-13 neon indicator tube is 14.7 years under continuous operation. The tube will still work after this period but its brightness will be less than 30% of the initial. We also found that the initial sputtering done at the time of manufacturing is equivalent to 26 weeks of normal operation.
The predicted usable life is very long due to several reasons. Firstly, the IN-13 tubes used by SALTechips also contain Argon gas which reduces the darkening rate. Secondly, we correctly drive the tube, preventing overdrive and avoiding constantly displaying the same value. Thirdly, the tube itself contains a mesh-grid electrode that reduces the darkening of the glass envelope.
And if 14.7 years is not enough, the display algorithm we have programmed in the thermNeon doubles the usable life to 29 years!
One additional point worth mentioning is that during the experiment we held illuminated length of the tube constant. Following the experiment, we have not been able to get the remaining length of tube to illuminate even if driving the tube with 15 mA (300% overdrive). This is due to severe cathode poisoning of the inactive portion of the cathode electrode. Therefore we cannot stress enough how important it is NOT to use these tubes in static displays. Thankfully the thermNeon takes care of this issue automatically, too.
The results are very significant and ever so relevant for nixie/neon indicator based products. To our knowledge this is the first time (at least in this century!) that the slow darkening of a neon indicator tube has been measured under realistic operating conditions and the data used to systematically determine the end of life of the tube. As such, we submit that these results and the underlying toolkit represent the state of the art and hope to see them applied to other types of indicator tubes.
The SHINE experiment and all of its idiosyncrasies have been tremendous fun over the 2.7 years that we acquired data. Even though this is the wrapping up for the SHINE experiment, we won’t stop here. We have ambitious plans for a laser-based active probing system to rapidly determine the end of life of nixie tubes, old and new 🙂
And don’t forget that we have open-sourced all raw measurement data and algorithm scripts (MATLAB®), so please get in touch with us via our main contact page or on social media. We are also keeping the test tube itself in a safe location should there be a need to go back and verify something.
References
Malev, M. D. (1972). Gas absorption and outgassing of metals. Vacuum, 43-60.
Moraw, M. (1986). Analysis of outgassing characteristics of metals. Vacuum, 523-525.
Stocker, B. J. (1961). Cathode sputtering in inert-gas glow discharges. British journal of Applied Physics, 465.
Todd, J. B. (1955). Outgassing of Glass. Journal of Applied Physics.
Weston, G. F. (1968). Cold Cathode Glow Discharge Tubes. London: Ilifee Books Ltd.
Contingency Protocols
As we expected the experiment to take a very long time, we planned the following procedures in the case of special events that interrupted the normal flow of the experiment.
- Power cut
In the event of a power failure, all equipment including the live stream computer will switch off. When power is restored, sufficient time will be allowed for the equipment to warm up. The neon tube will be re-ignited and the counter restored to the time of the last measurement. The maximum time error is the sampling period, 1 week. During this period the amount of material expected to be sputtered is small, therefore the effect should be insignificant. The live link will be restored after the experiment. A note will be made in the data log.
- Loss of live stream
The live link will be restored as soon as possible. The down time may vary depending on what caused the initial failure (e.g. freezing of computer, power failure, broadband connection issue etc).
- Timer overflow
The experiment will continue normally. The indicated time will be added to the maximum number of minutes.
- Damaged tube under test
The damage will be investigated. If the damage was due to elapsed operating time then the end of life has been reached prior to loss of brightness. Alternatively the experiment will have to be restarted with a new tube.
- Instrumentation malfunction
The instrumentation will be repaired and the experiment will resume from the time of the last measurement. Depending on the nature of the malfunction a judgement will be made if recalibration of the apparatus or restart of the experiment is needed.
- Absence at time of measurement
The measurement will be performed remotely using the live link. If the live link is not available at the time, the measurement will be skipped. If upon return it is found that normal operation was interrupted, the relevant procedure will be followed.
- Move of apparatus
If the apparatus needs to be moved (e.g. lab move), the move will take place after a measurement. This scenario will otherwise be treated as a power cut. The new location will have similar ambient conditions.
Assumptions
- The failure mechanism that will occur first is loss of brightness due to metal deposition on the glass envelope. This has been accounted for in the contingency protocols.
- The measurement equipment experiences long-term drift that is insignificant compared to measured loss of brightness. The equipment was calibrated before and after the experiment.
- The measurement equipment is sufficiently linear within the operating region covered by this experiment. The linearity is guaranteed by design.
Noise sources (e.g. radiated interferences) or other sources of radiation (e.g. ionising radiation) reaching the detector are insignificant compared to the desired signal or sufficiently suppressed by the data point averaging scheme and the long duration of the experiment.




